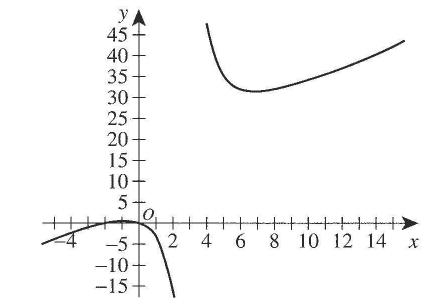
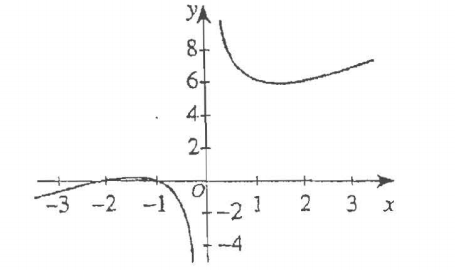
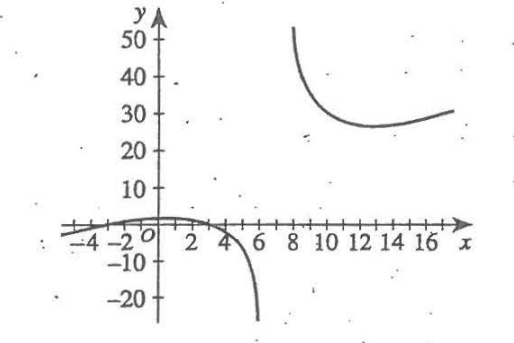
(5.) ACT The graph below shows the function $f(x) = \dfrac{2x - 5}{7x + 5}$ in the standard (x, y) coordinate
plane.
Which of the following is an equation of the horizontal asymptote of f(x)?
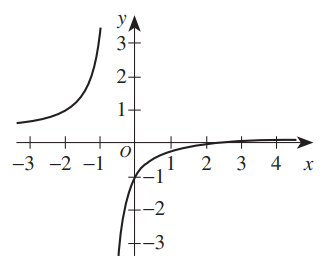
$ F.\;\; x = -1 \\[3ex] G.\;\; x = \dfrac{2}{7} \\[5ex] H.\;\; y = -1 \\[3ex] J.\;\; y = \dfrac{2}{7} \\[5ex] K.\;\; y = \dfrac{5}{7} \\[5ex] $
$ f(x) = \dfrac{2x - 5}{7x + 5} \\[5ex] \underline{Horizontal\;\;Asymptote:\;HA} \\[3ex] numerator\;\;in\;\;standard\;\;form ...yes \\[3ex] denominator\;\;in\;\;standard\;\;form ... yes \\[3ex] Degree\;\;of\;\;Numerator = Degree\;\;of\;\;Denominator = 1 \\[3ex] HA: y = \dfrac{leading\;\;coefficient\;\;of\;\;the\;\;numerator}{leading\;\;coefficient\;\;of\;\;the\;\;denominator} \\[5ex] HA: y = \dfrac{2}{7} $
Which of the following is an equation of the horizontal asymptote of f(x)?

$ F.\;\; x = -1 \\[3ex] G.\;\; x = \dfrac{2}{7} \\[5ex] H.\;\; y = -1 \\[3ex] J.\;\; y = \dfrac{2}{7} \\[5ex] K.\;\; y = \dfrac{5}{7} \\[5ex] $
$ f(x) = \dfrac{2x - 5}{7x + 5} \\[5ex] \underline{Horizontal\;\;Asymptote:\;HA} \\[3ex] numerator\;\;in\;\;standard\;\;form ...yes \\[3ex] denominator\;\;in\;\;standard\;\;form ... yes \\[3ex] Degree\;\;of\;\;Numerator = Degree\;\;of\;\;Denominator = 1 \\[3ex] HA: y = \dfrac{leading\;\;coefficient\;\;of\;\;the\;\;numerator}{leading\;\;coefficient\;\;of\;\;the\;\;denominator} \\[5ex] HA: y = \dfrac{2}{7} $
(6.) ACT In the standard (x, y) coordinate plane, the graph of which of the following equations has the line $x = 2$ as
a vertical asymptote?
$ A.\;\; y = \dfrac{4x + 3}{2x} \\[5ex] B.\;\; y = \dfrac{4x + 3}{x + 2} \\[5ex] C.\;\; y = \dfrac{4x + 3}{x - 2} \\[5ex] D.\;\; y = \dfrac{x + 2}{4x + 3} \\[5ex] E.\;\; y = \dfrac{x - 2}{4x + 3} \\[5ex] $
To determine the vertical asymptote:
(1.) Simplify the function
(2.) Set the denominator to zero
(3.) Solve for $x$
$ All\;\;the\;\;functions\;\;are\;\;already\;\;simplified \\[3ex] Looking\;\;at\;\;the\;\;denominators: \\[3ex] x - 2 = 0 \\[3ex] x = 2 \\[3ex] Correct\;\;Option:\;\; C $
$ A.\;\; y = \dfrac{4x + 3}{2x} \\[5ex] B.\;\; y = \dfrac{4x + 3}{x + 2} \\[5ex] C.\;\; y = \dfrac{4x + 3}{x - 2} \\[5ex] D.\;\; y = \dfrac{x + 2}{4x + 3} \\[5ex] E.\;\; y = \dfrac{x - 2}{4x + 3} \\[5ex] $
To determine the vertical asymptote:
(1.) Simplify the function
(2.) Set the denominator to zero
(3.) Solve for $x$
$ All\;\;the\;\;functions\;\;are\;\;already\;\;simplified \\[3ex] Looking\;\;at\;\;the\;\;denominators: \\[3ex] x - 2 = 0 \\[3ex] x = 2 \\[3ex] Correct\;\;Option:\;\; C $